Anoma猜漲跌遊戲最高多少分？
之前搖中過紅球，今天來了次黃球，不知道上面還有嘛？
記得剛接觸零知識證明的時候了解過一個經典遊戲👇
A給盲人B左右手各放置一個球，這倆球除了顏色可能不同以外，其他都相同，包括重量，觸感等。B可以向A提問無數次，但問題不能與顏色有關，問盲人B如何做才能確定這倆球是同色還是不同色？
盲人B可以手背後，讓A看不見他的動作，然後B在背後把雙手的球交換或者不交換都可以，然後在拿到前面來，問A：我交換過球沒有。如果球是不同色，A肯定知道B是否交換過，如果是同色的球，A看不出來是否交換過，很有可能猜錯，這樣反復操作提問多次，只要A答錯一次，就可以確定倆球顏色相同。
遊戲：證明“兩個球異色”而不泄露各自顏色的具體值。 Anoma 中的 ZK 用途：證明“這組意圖與撮合滿足資產守恆+約束”而不泄露內部細節（金額、完整偏好）。
類比映射：
1⃣隱藏值：球的具體顏色 ↔ 帳戶精確餘額 / 意圖內部參數。
2⃣需公開的性質：是否異色 ↔ 撮合合法/餘額充分/約束滿足。
3⃣證明方式：可區分置換（交換是否可見） ↔ 零知識電路的約束可滿足性證明。 核心共同點：只暴露必要的布爾/約束真值，不暴露原始祕密。
Anoma 在真實鏈上用零知識證明把這一思想規模化：僅暴露‘撮合與約束成立’這一性質，而把意圖與資產細節保持私密，從而實現隱私與可驗證性的統一。

北京雨後現彩虹，一整條，很久沒見到了🌈 別人拍的

這輪以太坊小牛市，相信大家多多少少都回了些本🤣
有空查一下主錢包鏈上高危授權，紅色嘆號都取消掉
這些❗️不是之前被盜的協議，就是被安全協議舉報過
要不就是棄用的老合約，都把授權取消，以絕後患
取消授權傳送門：
鏈上gas很低，以太主網也不到0.1u，Tx+1=福報+1🤩

倒計時兩天：River Mart NFT 值得佔用你 2 分鍾
核心邏輯
🔸參與門檻極低：準備15u-20u等值資產（流程中可隨時贖回），實際鏈上gas+磨損成本0.2u
🔸可獲潛在權益： 24M River Points 分配池份額+ 未來生態潛在空投權重+瓜分1300USDT獎池
🔸用時快：2–5 分鍾完成（熟練2分鍾，新手按教程5分鍾搞定）。
🔸最後窗口期：進入 @River4fun 下一階段前的任務——River Mart NFT 鑄造。
教程如下👇
我給大家規劃出6條鏈，分別是BSC ARB B2 BASE @SonicLabs @build_on_bob 。一方面是gas低，且BOB和Base鏈均未發幣，Sonic還有二期空投，適當活躍一下
我以BSC鏈爲例演示如何獲取NFT，其他鏈步驟類似
鑄造傳送門：
操作步驟：先用 PancakeSwap 把價值15u的 BNB 換成 wBNB 並在活動頁抵押，按≥120% 抵押率（實際需≥約15U 價值）鑄造≥10 枚 satUSD
還款時如果 satUSD 差少量不能還款（平台按該方式收取鑄幣費），可在 Swap 頁面用少量 USDT 兌換補足再還
📢提醒注意，BOB鏈上的抵押物WBTC是舊合約，CFa3結尾，注意看清。
要鑄造第三階段的Mystery NFT，需要擁有4個任意NFT，並在任意鏈上持有至少10u

今晚 @ 怎麼了？我平時用yubikey 5 登入，剛才想上去看看bullrun，結果怎麼也登入不上去。清緩存，重啓都試了，裏面還有幾百u🤣 這還有救嘛？已在官網開單

之前 $Zora 不值錢，現在漲起來就是豪華豬腳飯
最近主網gas都在0.2-0.3，趁着低gas把主網的資金歸攏
想起來Zora漲價，把之前沒查的沒claim的都領了
回顧這些強VC領投的高融資項目，如果開盤價低挨錘
低位橫盤後都會拉升一波 $SUI $IP $SAHARA
雖然拿了空投，我依然看不慣Jacob的行事風格
感覺Zora在Artcoin那個階段Launchpad是能做起來的
Jacob當初卻選擇了佛系運營，讓市場自生自滅
現在只能期待Base帶帶Zora的社交屬性

感謝 @rtk17025 提供 Anoma quiz 解析參與機會
題幹3：Where does solver execution happen?
簡解：
解決者的執行發生在鏈外（Off-chain），並通過可驗證的方式確保其結果的有效性。這種設計降低了鏈上計算壓力，同時保持了可信性。
詳解：
1️⃣ On the consensus layer：錯誤。解決者的執行並不發生在共識層，而是鏈外。
2️⃣ Off-chain with provable validity：正確。鏈外執行能夠減少鏈上負擔，並通過零知識證明等技術確保結果的有效性。
3️⃣ In the validator mempool：錯誤。驗證者的內存池主要用於交易排序，與解決者執行無關。
4️⃣ Within state channels：錯誤。狀態通道是一種擴展機制，與解決者執行的具體位置無關。參考文件內容：
正確答案來源於《whitepaper.pdf》第2.1節關於“Validity predicates”的描述：
Validity predicates are an architecture for smart contracts which separate out cleanly the task of computing state transitions and the task of verifyi

Anoma quiz 題目解析，讓自己了解熟悉 @anoma 還有機會取得測試網邀請碼🤩
1、題幹 What’s the main user benefit of intent-based UX? 意圖驅動用戶體驗的主要用戶優勢是什麼？
2、簡解
🔹意圖驅動用戶體驗的核心在於用戶只需表達目標（意圖），而無需理解復雜的操作流程。
🔹這種設計通過聲明意圖簡化交互流程，提升用戶控制力和操作效率。
🔹意圖驅動設計適用於動態、靈活的交互場景，而非固定步驟或特定功能。
3、答案詳解
1️⃣ Familiar CLI menus
錯誤。命令行菜單（CLI menus）是一種界面設計方式，與意圖驅動設計的核心理念無關。我在原文並沒有定位到 "familiar CLI menus"（熟悉的命令行菜單）。這個選項是人爲添加的幹擾項，用來測試用戶對內容的理解
2️⃣ Declarative intent
正確。意圖驅動設計的核心是“聲明意圖”（Declarative intent），用戶只需表達目標（如“轉移資產”或“進行交易”），系統會根據意圖匹配解決方案。這種方式簡化了用戶交互流程，提升了操作效率和用戶體驗👍
參考文件內容來源於文檔《whitepaper.pdf》第2.1節“Intent-centricity”部分👇
這句話的意思：
意圖是用戶與應用程序交互的核心點。通過“意圖驅動

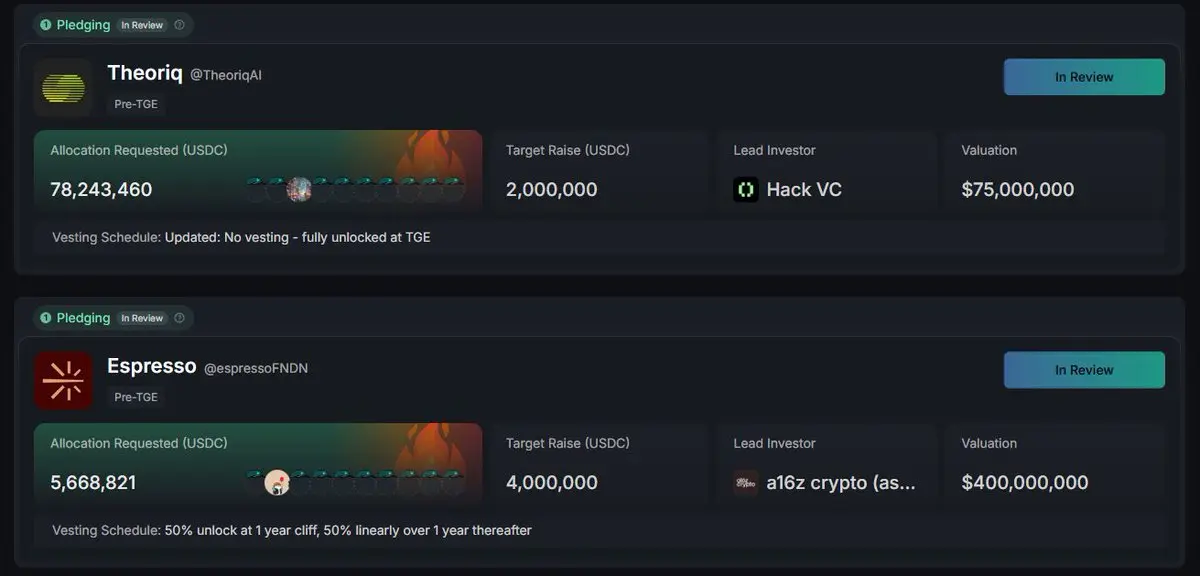
KAITO 啓動板的第一批項目 @TheoriqAI 和 @EspressoSys 申購階段已結束，總共質押了約8400萬美金，兩者都超額認購🥳
現在進入審核階段，團隊會根據社交聲譽、鏈上持倉（不僅限於Kaito持倉）、與項目及相關領域的歷史一致性/相關性、認購意願、質押金額，甚至地域等多方面因素來決定分配。
也就是項目方選人階段，看綜合貢獻和過往經歷吧。地域是什麼個情況？歐美給的多？還是地方越窮給的越多，助你翻身？🤣如果沒被選中，質押的金額會原路退還。
Espresso：7月31日公布分配結果，分配階段到8月4日結束。
Theoriq：8月5日公布分配結果，沒有分配階段，因爲質押金額已經超過目標。

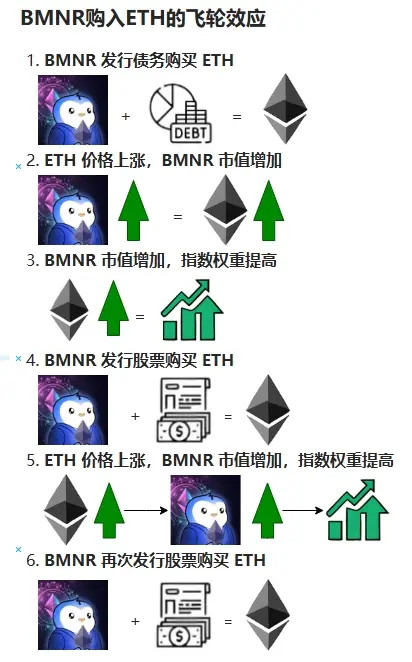
BMNR @BitMNR 宣布其 $ETH 持有量已突破 56 萬枚，總價值超過 20 億美元。公司目標是獲取並質押整體 ETH 供應量的 5%。目前 ETH 總市值爲 4,397 億美元，這意味着公司還需增持約 200 億美元的 ETH
有Peter Thiel ，Tom Lee，木頭姐坐鎮的BMNR大概率復制當年微策略的路數，和Lubin的Sharplink Gaming 一路高歌買買買👇