# 探索Circle STARKs近年來,STARKs協議設計的趨勢是轉向使用較小的字段。最早期的STARKs實現使用256位字段,但這種設計效率較低。爲解決這個問題,STARKs開始使用更小的字段,如Goldilocks、Mersenne31和BabyBear。使用小字段提升了證明速度,但也帶來了新的挑戰。例如,在小字段中選擇隨機點時,可選範圍變小,容易被攻擊者破解。爲此,需要採取額外措施來增強安全性。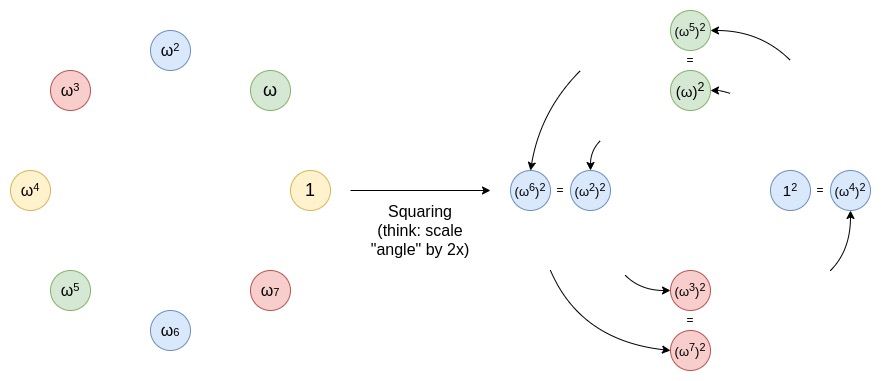Circle STARKs是一種新的解決方案。它使用了一種特殊的羣結構,可以在Mersenne31等小字段上實現高效的FRI協議。Circle STARKs的核心是利用圓羣的幾何性質,將二維空間上的運算映射到一維空間,從而提高計算效率。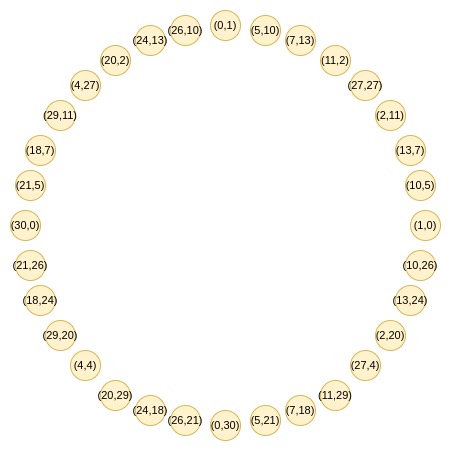Circle STARKs還支持Circle FFT,這是一種特殊的FFT算法。與常規FFT不同,Circle FFT處理的是Riemann-Roch空間上的函數,而不是嚴格意義上的多項式。這種差異雖然在數學上很復雜,但對開發者來說幾乎可以忽略不計。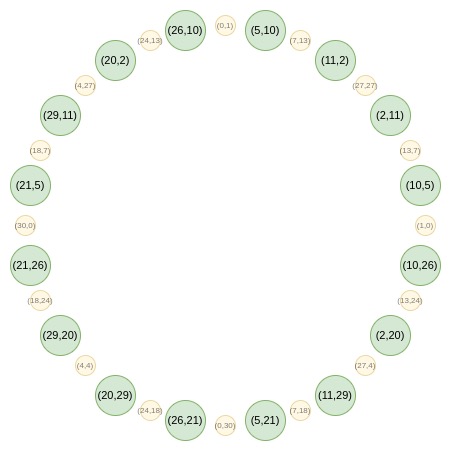在實現細節上,Circle STARKs與常規STARKs有一些不同,如商運算、消失多項式、反向位序等。但總的來說,Circle STARKs對開發者而言並不比常規STARKs復雜多少。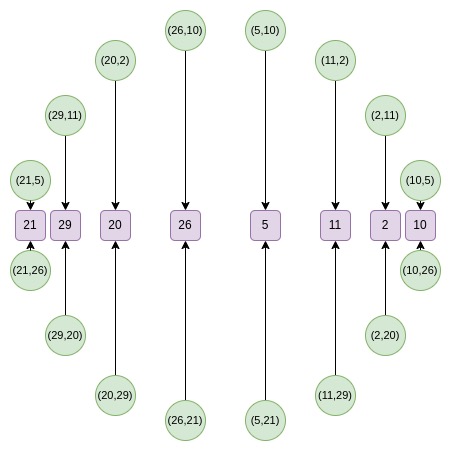Circle STARKs結合Mersenne31字段,可以實現非常高效的證明。它在計算跟蹤中充分利用了空間,減少了浪費。雖然Binius等方案在某些方面更優,但Circle STARKs概念簡單,易於理解和實現。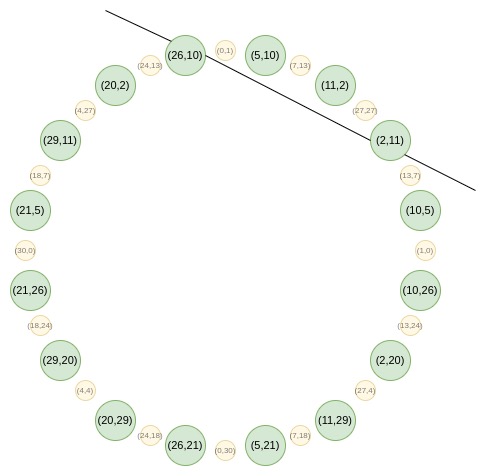隨着STARKs基礎層效率接近極限,未來的優化方向可能包括:優化密碼學原語的算術化、使用遞歸構造提高並行性、改進虛擬機的算術化以提升開發體驗等。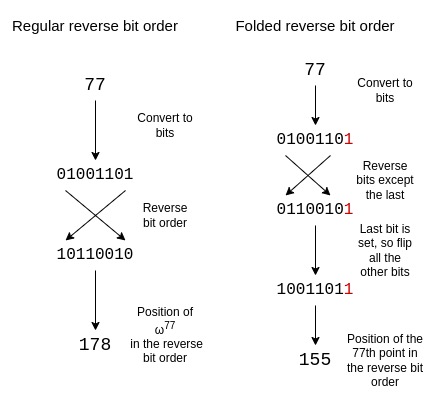
Circle STARKs: 小字段高效證明的新解決方案
探索Circle STARKs
近年來,STARKs協議設計的趨勢是轉向使用較小的字段。最早期的STARKs實現使用256位字段,但這種設計效率較低。爲解決這個問題,STARKs開始使用更小的字段,如Goldilocks、Mersenne31和BabyBear。
使用小字段提升了證明速度,但也帶來了新的挑戰。例如,在小字段中選擇隨機點時,可選範圍變小,容易被攻擊者破解。爲此,需要採取額外措施來增強安全性。
Circle STARKs是一種新的解決方案。它使用了一種特殊的羣結構,可以在Mersenne31等小字段上實現高效的FRI協議。Circle STARKs的核心是利用圓羣的幾何性質,將二維空間上的運算映射到一維空間,從而提高計算效率。
Circle STARKs還支持Circle FFT,這是一種特殊的FFT算法。與常規FFT不同,Circle FFT處理的是Riemann-Roch空間上的函數,而不是嚴格意義上的多項式。這種差異雖然在數學上很復雜,但對開發者來說幾乎可以忽略不計。
在實現細節上,Circle STARKs與常規STARKs有一些不同,如商運算、消失多項式、反向位序等。但總的來說,Circle STARKs對開發者而言並不比常規STARKs復雜多少。
Circle STARKs結合Mersenne31字段,可以實現非常高效的證明。它在計算跟蹤中充分利用了空間,減少了浪費。雖然Binius等方案在某些方面更優,但Circle STARKs概念簡單,易於理解和實現。
隨着STARKs基礎層效率接近極限,未來的優化方向可能包括:優化密碼學原語的算術化、使用遞歸構造提高並行性、改進虛擬機的算術化以提升開發體驗等。